В статистике имеют большое значение индексы переменного и фиксированного состава, которые используются при анализе динамики средних показателей.

Индивидуальный индекс ФОП отражает изменение выпуска продукции одного вида и определяется по формуле:

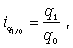(1)

где q₁ и q₀ — количество продукции данного вида в натуральном выражении в текущем и базисном периодах.

Агрегатный индекс ФОП (предложен Э. Ласпейресом) отражает изменение выпуска всей совокупности продукции, где индексируемой величиной является количество продукции q, а соизмерителем — цена р:

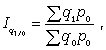(2)

где q₁ и q₀ — количество выработанных единиц отдельных видов продукции соответственно в отчетном и базисном периодах;

p₀ — цена единицы продукции (отдельного вида) в базисном периоде.

При вычислении индекса ФОП в качестве соизмерителей может выступать также себестоимость продукции или трудоемкость.

Средние взвешенные индексы ФОП используются в том случае, если известны индивидуальные индексы объема по отдельным видам продукции и стоимость отдельных видов продукции (или затраты) в базисном или отчетном периоде.

Средний взвешенный арифметический индекс ФОП определяется по формуле

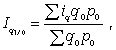(3)

где i_q — индивидуальный индекс по каждому виду продукции;

q₀ p₀ — стоимость продукции каждого вида в базисном периоде.

Средний взвешенный гармонический индекс ФОП:

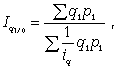(4)

где q₁ p₁ — стоимость продукции каждого вида в текущем периоде.

Индивидуальный индекс ЗВП отражает изменение затрат на производство одного вида и определяется по формуле

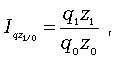(5)

где z₁ и z₀ — себестоимость единицы продукции искомого вида в текущем и базисном периодах;

q₁ z₁ и q₀ z₀ — суммы затрат на выпуск продукции искомого вида в текущем и базисном периодах.

Агрегатный индекс ЗВП характеризует изменение общей суммы затрат на выпуск продукции за счет изменения количества выработанной продукции и ее себестоимости и определяется по формуле

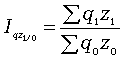(6)

где q₁ z₁ и q₀ z₀ — затраты на выпуск продукции каждого вида соответственно в отчетном и базисном периодах.

Рассмотрим построение индекса стоимости продукции (СП), который может определяться и как индивидуальный, и как агрегатный.

Индивидуальный индекс СП характеризует изменение стоимости продукции данного вида и имеет вид:

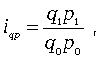(7)

где p₁ и p₀ — цена единицы продукции данного вида в текущем и базисном периодах;

q₁ p₁ и q₀ p₀ — стоимость продукции данного вида в текущем и базисном периодах.

Агрегатный индекс СП (товарооборота) характеризует изменение общей стоимости продукции за счет изменения количества продукции и цен и определяется по формуле:

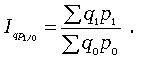(8)

Самым распространенным индексом в этой группе является индекс цен.

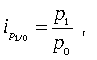(9)

где p₁ и p₀ — цена за единицу продукции в текущем и базисном периодах.

Соответственно определяются индексы себестоимости и затрат рабочего времени по каждому виду продукции.

Агрегатный индекс цен определяет среднее изменение цены р по совокупности определенных видов продукции q.

Для характеристики среднего изменения цен на потребитель-ские товары используют индекс цен, предложенный Э. Ласпейресом (индекс Ласпейреса):

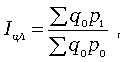(10)

где q₀ — потребительская корзина (базовый период);

p₀ и p₁ — соответственно цены базисного и отчетного периодов.

Если количество набора продуктов принимается на уровне отчетного периода (q₁ ), то в этом случае индекс цен именуется индексом Пааше:

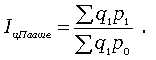(11)

Если известны индивидуальные индексы цен по отдельным видам продукции и стоимость отдельных видов продукции, то применяются средние взвешенные индексы цен (средний взвешенный арифметический и средний взвешенный гармонический индексы цен).

Формула среднего взвешенного арифметического индекса цен:

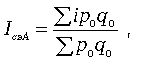(12)

где i — индивидуальный индекс по каждому виду продукции; p₀ q₀ — стоимость продукции каждого вида в базисном периоде.

Формула среднего взвешенного гармонического индекса цен

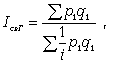(13)

где p₁ q₁ — стоимость продукции каждого вида в текущем периоде.

В статистической практике очень широко используется агрегатный территориальный индекс цен, который может быть рассчитан по следующей формуле:

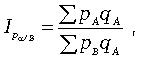(14)

где p_A p_B — цена за единицу продукции каждого вида соответственно на территории А и В;

q_A — количество выработанной или реализованной продукции каждого вида по территории А (в натуральном выражении).

Из формулы видно, что в данном индексе в качестве фиксированного показателя (веса) принят объем продукции территории А. При расчете данного индекса в качестве веса можно принять также объем продукции территории В или суммарный объем продукции двух территорий.

Возможны два способа расчета индексов: цепной и базисный.

В качестве примера можно привести цепные и базисные индексы цен.

Цепные индивидуальные индексы цен имеют следующий ряд расчета:

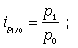
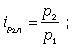
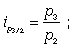  … . (15)

Базисные индивидуальные индексы цен:

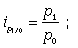
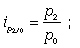
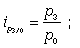  … . (16)

Следует помнить, что произведение цепных индивидуальных индексов цен равно последнему базисному индексу:

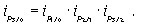(17)

Цепные агрегатные индексы цен:

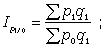
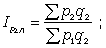
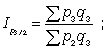  … . (18)

Базисные агрегатные индексы цен:

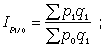
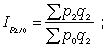
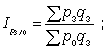  … . (19)

Между индексами существует также взаимосвязь и взаимозависимость, как и между самими экономическими явлениями, что позволяет проводить факторный анализ. Благодаря индексному методу можно рассматривать все факторы независимо друг от друга, что дает возможность определить размер абсолютного изменения сложного явления за счет каждого фактора в отдельности.

Предположим, что результативный признак зависит от трех факторов и более. В этом случае результативный индекс примет вид:

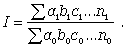(20)

Изменение результативного индекса за счет каждого фактора может быть выражено следующим образом:

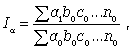
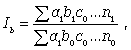
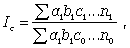
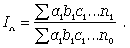  (21)

Для выявления роли каждого фактора в отдельности индекс сложного показателя разлагают на частные (факторные) индексы, которые характеризуют роль каждого фактора. При этом используют два метода:

метод обособленного изучения факторов;

последовательно-цепной метод.

При первом методе сложный показатель берется с учетом изменения лишь того фактора, который взят в качестве исследуемого, все остальные остаются неизменными на уровне базисного периода.

Последовательно-цепной метод предполагает использование системы взаимосвязанных индексов, которая требует определенного расположения факторов. Как правило, на первом месте в цепи располагают качественный фактор. При определении влияния первого фактора все остальные сохраняются в числителе и знаменателе на уровне базисного периода, при определении второго факторного индекса первый фактор сохраняется на уровне базисного периода, а третий и все последующие — на уровне отчетного периода, при определении третьего факторного индекса первый и второй факторы сохраняются на уровне базисного периода, четвертый и все остальные — на уровне отчетного периода и т.д.

Задача 1

Произвести анализ 15 самых надежных среди малых и средних коммерческих банков одного из регионов применяя метод группировок.

В качестве группировочных признаков выберите уставный капитал, образуя 4 группы банков с равными интервалами.

По каждой группе посчитать:

1. число банков
   
2. работающие активы, уставный капитал
   
3. в среднем на один банк капитал и работающие активы
   

   Результаты расчетов сведите в таблицу.
   

   Сделайте выводы.
   

    

    

   Решение
   

    

   Вначале определяем размах вариации по следующей формуле:
   

   R = Х_max – Х_min = 23000 – 1579 = 21421
   

   2. Определим величину интервала
   

   i = R/4 = 21421/4=5355,25
   

   3. Строим вспомогательную таблицу:
   

   Таблица 2 – Вспомогательная таблица группировки банков по уставному капиталу
   

   Группа предприятия	Номер банка	Уставный капитал	Капитал	Работающие активы
   I 1579– 6934,25	8	1579	5897	6089
   	1	1824	18758	10500
   	4	2089	67888	40256
   	13	2245	8153	16663
   	3	2626	9273	40256
   	10	3484	10276	10099
   	15	3572	23459	31717
   	7	5265	24236	25595
   	9	6799	38290	79794
   II 6934,25 – 12289,5	12	8973	20702	21165
   	14	9063	10215	9115
   III 12289,5 – 17644,75	11	13594	35662	30005
   	6	17489	53255	82795
   IV 17644,75– 23000	5	23000	24654	29007
   å	15	99513	350718	433056

    

   По каждой группе банков произведем расчет число банков, работающие активы, уставный капитал, в среднем на один банк капитал и работающие активы, используя формула для расчета среднего значения признака по формуле:
   

   
   

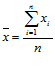
   Таблица 3 – Расчеты по каждой сгруппированной группе банков числа банков, работающих активов, уставного капитала, в среднем на один банк капитал и работающие активы
   

   Группа предприятия	Число банков, n	Величина уставного капитала	Капитал	Работающие активы
   I 1579– 6934,25	9	29483	206230	260969
   Средняя величина на группу		3275,9	22914,4	28996,6
   II 6934,25 – 12289,5	2	18036	30917	30280
   Средняя величина на группу		9018	15458,5	15140
   III 12289,5 – 17644,75	2	31083	30917	112800
   Средняя величина на группу		15541,5	15458,5	56400
   IV 17644,75– 23000	1	23000	24654	29007
   Средняя величина на группу		23000	24654	29007
   å	15	6634,2	23381,2	28870,4

    

   Вывод: Как видим в данной группе наибольшее количество составляют малые банки – 9, их средний уставной капитал составляет 3275,9 тыс. руб., у этой группы самые наименьшие величины среднего значения работающих активов – 28996,6 тыс. руб., но они имеют самое большое значение капитала – 206230 тыс. руб., наименьшее число банков в 4-ей группе – 1 банк, в двух остальных группах – двум банкам. Наибольшее значение среднего уставного капитала у 4-й группы – 23000 тыс. руб.
   

    

    

   Задача 2
   

    

   Распределение рабочих предприятия по тарифному разряду имеет следующий вид:
   

    

   Таблица 4– Исходные данные
   

   Тарифный разряд	Число рабочих, чел.
   1	10
   2	15
   3	12
   4	50
   5	25
   6	8

    

   1. определите средний уровень квалификации рабочих предприятия
   

   2. укажите какие виды средних нужно применять для вычисления этих показателей.
   

    

   Решение
   

    

   Для вычисления данных показателей следует использовать форму арифметической взвешенной:
   

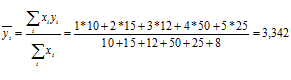   ≈ 4 разряд
   

   где х_i – число рабочих, чел.
   

   y_i – тарифный разряд.
   

   Можно также найти рассчитываемый показатель и как среднее арифметическое:
   

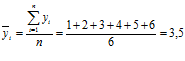   ≈ 4 разряд
   

   Можно также рассчитать по формуле средней геометрической
   

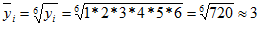   разряд
   

    

   По формуле средней квадратичной
   

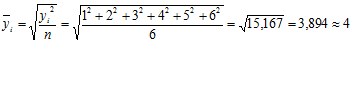   разряд
   

   По формуле гармонической взвешенной
   

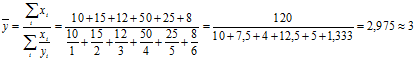   разряд
   

   Как видим, наиболее близкие значение средних рассчитанных по формуле средней квадратичной, среднее арифметическое, арифметической взвешенной и примерно дают один и тот же результат – 4 разряд. Формулы среднегеометрической, гармонической взвешенной нельзя использовать, так как полученные по ней результат существенно отличается.
   

   Следовательно, более точные и верные результаты получены при расчете по формуле арифметической взвешенной и средней квадратичной.
   

    

    

    

    

    

    

    

    

    

    

    

    

   Задача 3
   

    

   Производство нефти характеризуют следующие данные:
   

    

   Таблица 5– Исходные данные
   

   Годы	2001	2002	2003	2004	2005
   Нефть, тыс. тонн	153	159	166	170	172

    

   Для анализа динамики производства нефти вычислите:
   

   – абсолютные приросты, темпы роста и темпы прироста по годам (цепные) и к базисному 2001 году, абсолютное содержание 1% прироста. Полученные данные сведите в таблицу;
   

   – средний уровень ряда
   

   – среднегодовой темп роста
   

   Представьте динамику производства нефти на графике.
   

    

   РЕШЕНИЕ
   

   1. Абсолютный прирост определяется по формуле (тыс. тонн):
   

   А_iб = y_i – y₀
   

   А_iц = y_i – y_i-1
   

   2. Темп роста определяется по формуле (%):
   

   Т_рб = (y_i / y₀) *100
   

   Т_рц = (y_i / y_i-1)*100
   

   3. Темп прироста определяется по формуле (%):
   

   Т_nрб = Т_рб –100%:
   

   Т_nрц = Т_рц – 100%
   

   4. Средний абсолютный прирост:
   

   
   

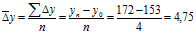
   y_n – конечный уровень динамического ряда;
   

   y₀ – начальный уровень динамического ряда;
   

   n – число цепных абсолютных приростов.
   

   5. Среднегодовой темп роста:
   

   
   

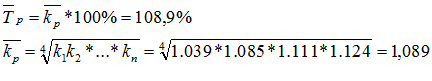
   6. Среднегодовой темп прироста:
   

   
   

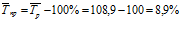
   3) Абсолютное содержание 1% прироста (тыс . тонн):
   

   А = Aiц / Т_рiц
   

   4) Средний уровень динамики рассчитывается по формуле
   

   
   

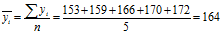
   Полученные данные сведем в таблицу
   

   Таблица – Результаты расчетов анализа динамики маргариновой продукции
   

   Показатели	Годы
   	2001	2002	2003	2004	2005
   1. Производство сахара-песка, тыс. тонн.	153	159	166	170	172
   2. Абсолютный прирост	—
   Aib	—	6	13	17	19
   Aiц	—	6	7	4	2
   3. Темп роста	—
   Трib	—	103,9	108,5	111,1	112,4
   Трiц	—	103,9	104,4	102,4	101,2
   4. Темп прироста	—
   Тпib	—	3,9	8,5	11,1	12,4
   Тпiц	—	3,9	4,4	2,4	1,2
   5. Значение 1% прироста	—	1,53	1,59	1,66	1,7

    

   Представим динамику производства сахара-песка на графике
   

    

   
   

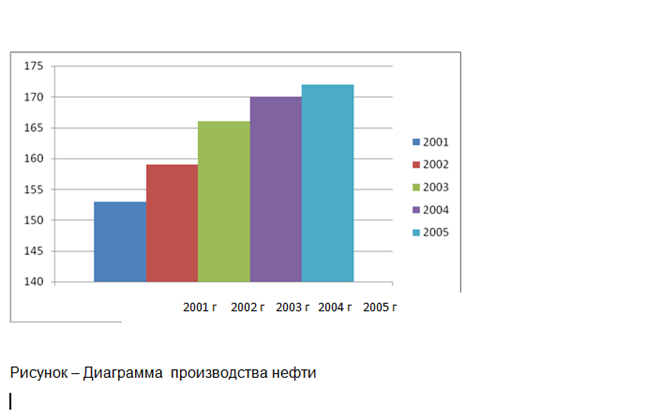
   Таким образом, отмечается положительная динамика роста производства нефти.
   

    

    

    

    

    

    

    

    

    

    

    

    

    

    

    

    

   Задача 4
   

    

   По себестоимости и объему продукции двух предприятия характеризуют следующие данные.
   

    

   Таблица – Исходные данные
   

   № завода	Изделия	Себестоимость единицы изделия, тыс руб.		Выработано продукции, тыс.шт.
   		Базисный период	Отчетный период	Базисный период	Отчетный период
   1	«А»	90	93	630	600
   	«Б»	120	110	450	500
   2	«А»	80	81	450	810

    

   1. На основании приведенных данных для завода № 1 вычислите:
   

   – общий индекс себестоимости;
   

   – общий индекс затрат на продукцию;
   

   2. Для двух заводов вместе (по изделию «А») вычислите индексы себестоимости: переменного состава; постоянного состава; структурного сдвига.
   

   Объяснить разницу между величиной индекса переменного и постоянного состава.
   

    

   Решение
   

    

   Для вычисления составим вспомогательную таблицу.
   

    

   Таблица – Вспомогательная таблица
   

   Изделия завода № 1	Себестоимость единицы продукции		Выработано продукции, тыс. ед		Себестоимость всего объема выработки		Условные величины
   	Базисный период	Отчетный период	Базисный период	Отчетный период	Базисный период	Отчетный период	q1 p0	q0 p1
   	p0	p1	q0	q1	q0 p0	q1 p1
   «А»	90	93	630	600	56700	55800	54000	58590
   «Б»	120	110	450	500	54000	55000	60000	49500
   Всего					110700	110800	114000	108090

    

   Рассчитаем общие индексы физического объема продукции:
   

   по формуле Ласпейреса
   

   
   

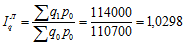
   по формуле Пааше
   

   
   

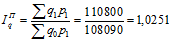
   по формуле Фишера
   

   
   

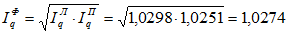
   Таким образом, в отчетный период по сравнению с базовым в целом наблюдается рост объемов физического объема продукции в натуральном выражении на 2,98% – по формуле Ласпейреса, на 2,51% по формуле Паше. Общий индекс физического объема равен 1,0274, что говорит о росте физического объема продукции в отчетном году по сравнению с базисным на 2,74%.
   

   Определим значения сводных индексов себестоимости продукции
   

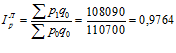   или 97,64%
   

   
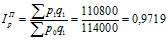   или 97,19%
   

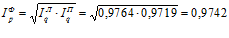   или 97,42%
   

   Следовательно, в отчетном году наблюдается снижение себестоимости на весь объем выпускаемых изделий по формуле Ласпейреса на 2,36%, по формуле Пааше – на 2,81% и на 2,58% по формуле Фишера. Соответственно, изменилась и величина затрат на продукцию за счет роста себестоимости всего объема выпускаемого продукции.
   

   Сводный индекс затрат на продукцию равен
   

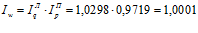   или 0,01%
   

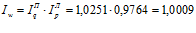   или 0,09%
   

   Таким образом, общий индекс затрат равный 1,0001 определяет что величина затрат на продукцию вырос на 0,01%.
   

   2. Рассчитаем для двух заводов вместе (по изделию А) индексы себестоимости переменного состава, постоянного состава; структурного сдвига.
   

   Составим вспомогательную таблицу
   

    

   Таблица – Вспомогательная таблица
   

   Изделия завода № 1	Себестоимость единицы продукции		Выработано продукции, тыс. ед		Себестоимость всего объема выработки		Удельные веса,
   	Базисный период	Отчетный период	Базисный период	Отчетный период	Базисный период	Отчетный период	Базисный период. d0	Отчетный период d1
   	p0	p1	q0	q1	q0 p0	q1 p1
   «А»	90	93	630	600	56700	55800	0,6117	0,4596
   «А»	80	81	450	810	36000	65610	0,3883	0,5404
   Всего					92700	121410	1,0	1,0

    

   а) индекс переменного состава представляет собой соотношение средних величин какого-либо признака в отчетном и базисном периодах.
   

   Расчет ведем по формуле, в которой в качестве весов используются удельные веса единиц совокупности в общей численности совокупности – d.
   

   
   

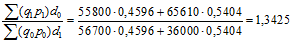
   б) индекс постоянного состава строится как отношение взвешенных величин постоянного состава. Расчет также ведем с помощью удельных весов единиц совокупности в общей численности совокупности – d:
   

   
   

    

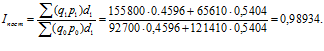
   в) индекс структурных сдвигов характеризует влияние изменения структуры изучаемой совокупности на динамику среднего уровня признака по формуле
   

   
   

    

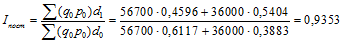
   Разницу между величиной индекса переменного и постоянного состава можно объяснить тем, что индекс переменного состава равнее отношению средних уровней индексируемых величин отчетного и базисного периода и отражает не только изменение усредняемого показателя, но и изменение состава данной совокупности, а индекс постоянного состава отражает изолированное действие признака.
   

    

   список литературы
   

    

    

4. Общая теория статистики / Под ред. И.Н. Елисеевой. –М.: Финансы и статистика, 2009.
   
5. Статистика: Курс лекций /Харченко Л.П., Долженкова В.Г., Ионина В.Г./-М.: ИНФРА-М, 2006.
   
6. Тарновская Л.И. Статистика. –М.: Академия, 2008.
   
7. Рыбаковский О. Л. Теория статистики. –М.: РАГС, 2008.